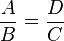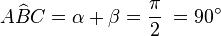desventajas de las redes sociales

Actividades

Teorema de Tales

 

Existen dos teoremas relacionados con la geometría clásica que reciben el nombre de teorema de Tales, ambos atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.

Los dos teoremas de Tales

Semicírculo que ilustra el segundo teorema de Tales.

El primero de ellos explica esencialmente una forma de construir un triángulo semejante a uno previamente existente ("los triángulos semejantes son los que tienen ángulos iguales y sus lados homólogos proporcionales"). Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos ("encontrándose estos en el punto medio de su hipotenusa"), que a su vez en la construcción geométrica es ampliamente utilizado para imponer condiciones de construcción de ángulos rectos. Si tres o más rectas paralelas son intersecadas cada una por dos transversales, los segmentos de las transversales determinados por las paralelas, son proporcionales.

Primer teorema

Una aplicación del teorema de Tales.

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:

Teorema primero Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado. Tales de Mileto

Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.

Corolario

Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.
Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, del mismo se deduce a modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:

Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de la pirámide de Keops en Egipto. En cualquier caso, el teorema demuestra la semejanza entre dos triángulos, no la constancia del cociente.
Del primer teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo): Si las rectas A, B, C son paralelas y cortan a otras dos rectas R y S, entonces los segmentos que determinan en ellas son proporcionales.

Segundo teorema

fig 2.1 Ilustración del enunciado del segundo teorema de Tales de Mileto.

El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:

Teorema segundo Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo. Tales de Mileto

Este teorema (véase fig 2.1 y 2.2), es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de los ángulos inscritos dentro de una circunferencia.

Demostración

fig 2.2 Siempre que AC sea un diámetro, el ángulo B será constante y recto.

fig 2.3 Los triángulos AOB y BOC son isósceles.

En la circunferencia de centro O y radio r (véase fig 2.3), los segmentos

OA , OB y OC

son iguales por ser todos radios de la misma circunferencia.
Por lo tanto los triángulos AOB y BOC son isósceles.
La suma de los ángulos del triángulo ABC es:

Dividiendo ambos miembros de la ecuación anterior por dos, se obtiene:

Con la expresión anterior el segundo teorema queda demostrado.

Corolarios

(Corolario 1) En todo triángulo rectángulo la longitud de la mediana correspondiente a la hipotenusa es siempre ½ de la hipotenusa.”

Ya que aplicando el teorema anterior, se sabe que para cualquier posición que adopte el vértice B vale la igualdad, OA = OB = OC = r, donde OB es la mediana de la hipotenusa, (véase fig 2.3).

(Corolario 2) “La circunferencia circunscripta a todo triángulo rectángulo siempre tiene radio igual a ½ de la hipotenusa y su circuncentro se ubicará en el punto medio de la misma.”

El corolario 2 también surge de aplicar el teorema anterior, para una comprensión intuitiva basta observar la fig 2.2.

Aplicación (Tales - teorema segundo)

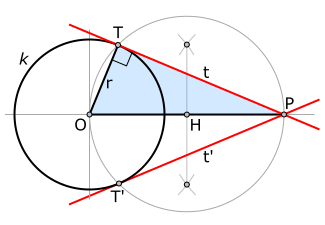
Construcción de tangentes (líneas rojas) a una circunferencia k desde un punto P, utilizando el «segundo teorema de Tales».

El “segundo teorema” (de Tales de Mileto) puede ser aplicado para trazar las tangentes a una circunferencia k dada, que además pasen por un punto P conocido y externo a la misma (véase figura).
Se supondrá que una tangente cualquiera t (por ahora desconocida) toca a la circunferencia k en un punto T (también desconocido por ahora). Se sabe por simetría que cualquier radio r de la circunferencia k es perpendicular a la tangente del punto T que dicho radio define en la misma, por lo que concluimos que ángulo OTP es necesariamente recto.
Lo anterior implica que el triángulo OTP es rectángulo. Recordando el «corolario 2 del teorema segundo de Tales» podemos deducir que entonces el triángulo OTP es inscribible en una circunferencia de radio ½ de la hipotenusa OP del mismo.
Entonces marcando el punto H como punto medio de la hipotenusa OP y haciendo centro en el mismo, podemos dibujar una segunda circunferencia auxiliar (gris en la figura) que será la que circunscribe al triángulo OTP.
Esta última circunferencia trazada se intersecará con la circunferencia k en dos puntos T y T', estos son justamente los puntos de tangencia de las dos rectas que son simultáneamente tangentes a k y además pasan por el punto P, ahora ya conocidos los puntos T y T' solo basta trazar las rectas TP y T'P (rojas en la figura) para tener resuelto el problema.

Leyenda

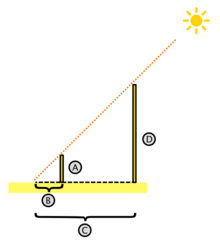
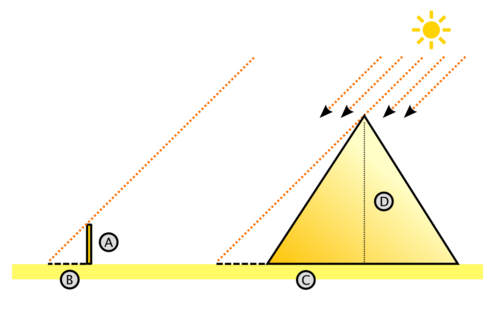
Según la leyenda (relatada por Plutarco),¹ Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza (las de Keops, Kefrén y Micerino), construidas varios siglos antes. Admirado ante tan portentosos monumentos de esta civilización, quiso saber su altura. De acuerdo a la leyenda, trató este problema con semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos), pudo establecer una relación de semejanza (teorema primero de Tales) entre dos triángulos rectángulos, por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (conocible) y la longitud de su altura (desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) cuyos catetos conocibles (A y B) son, la longitud de la vara y la longitud de su sombra. Realizando las mediciones en una hora del día en que la sombra de la vara sea perpendicular a la base de la cara desde la cual medía la sombra de la pirámide y agregando a su sombra la mitad de la longitud de una de las caras, obtenía la longitud total C de la sombra de la pirámide hasta el centro de la misma.

Como en triángulos semejantes, se cumple que 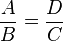, por lo tanto la altura de la pirámide es 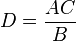, con lo cual resolvió el problema.

Actividades

Situación 1:
En una práctica de tiro, se coloca una barrera de 2m de alto a 3m de un blanco. Para disparar, el tirador debe subirse a un poste que está a 10m del pie de la barrera. ¿Desde qué altura mínima debe disparar para poder dar en el blanco?


Situación 2:
Encuentra la altura del árbol utilizando una varilla de 0,4 m de longitud, si se conoce que la sombra del árbol es de 6m y la sombra de la varilla es de 1m.


Situación 3:
En el triángulo AWG, los segmentos KQ y AG son paralelos, el segmento AK = 4, KW = 8 y GQ = 5. Encuentra la longitud del segmento WQ.


Situación 4:
A este poste se le puede calcular la altura.

Arma tu equipo con tres compañeros más y busca situaciones como esta en tu institución y calcula la altura utilizando el Teorema de Thales.
Realiza un vídeo con todas las acciones ejecutadas, parecido al que se encuentra en Aplicaciones. También puedes tomar fotos como evidencia de tu trabajo.
Tu celular y cámara fotográfica te serán de mucha ayuda, no dudes en enviar, ya sea por correo o por bluetooth cuando estemos trabajando en clase, tus fotos y videos para subirlos en la web.

viernes, 24 de julio de 2009

A cerca de thales

Curiosidades sobre Thales.
Thales es recordado principalmente por su cosmología basada en el agua como esencia de toda materia y por su predicción del eclipse de sol, que debió ocurrir el 28 de mayo de 585 a. C. Lo espectacular de esta predicción es que detuvo la batalla entre Alyattes y Cyaxares en ese año. Es probable que el hecho de que el eclipse fuera total y la localidad afectada correspondiera a la de una batalla importante contribuyera enormemente a la reputación de Thales como astrónomo.
Thales fué el primero en sostener que la luna brillaba por el reflejo del sol y además determinó el número exacto de días que tiene el año.
Thales también fué el famoso sabio de la historia que cayó en un pozo por mirar las estrellas y una anciana le dijo: "pretendes observar las estrellas y ni siquiera ves lo que tienes a tus pies". También se le atribuye a Thales la historia del mulo que cargaba sal y que se metía en el río para disolverla y así aligerar su peso; Thales le quitó esa mala costumbre cargándolo con esponjas.
Cuando le preguntaron sobre la recompensa que quería por sus descubrimientos, contestó: "me consideraría bien recompensado si los demás no se atribuyeran mis hallazgos, sino que reconocieran que son míos".


Citas de Thales.
- Busca una sola sabiduría.
- Elige una sola cosa buena.
- Lo más grande es el espacio, porque lo encierra todo.
- Lo más veloz es el entendimiento, porque corre por todo.
- Lo más fuerte es la necesidad, porque domina todo.
- Lo más sabio es el tiempo, porque esclarece todo.
- Conocéte a ti mismo.


Observa el siguiente video que trata sobre la leyenda del Teorema de Thales de Mileto.

Reflexiona acerca de los siguientes interrogantes:

¿Puedes describir mediante un dibujo la técnica que utilizó Thales para medir la altura de la pirámide?.